Okay, there are times when one has to deliver bad news and this is one of them. It’s a long believed and taught methodology that cost averaging into the stock market is a wise decision. The reason this is thought to be true makes partial sense. Say for instance that I have just won €100.000 Euro in the Lottery. That’s about $140,000 dollars in U.S. currency in today’s exchange rates. My financial advisor says, don’t invest it all at once but put €10.000 in the market each month for 10 months. For American readers, in Europe they use commas where we use periods and vice versa for denoting numbers in powers of one thousand.
Now, the reasoning of this strategy makes sense to most of us, because we are told, if you invest €10.000 each month into some company or mutual fund and the shares that month say are €1.000 you buy 10 shares. Next month if the share price drops 10% to €900, you’d buy 11.11 shares (if you could buy partial shares like for a mutual fund instead of some stock). Then if in the month after you invest €10.000 when the share price rose to say €1.100 you buy 9.09 shares and so on. The net effect is that you’d be buying more shares when the price is lower and less shares when the price is higher so that on average you be getting the shares for less than the average price over the course of 10 months.
Now, this is all true and of course you get the same result when using this example in dollars. However, this only measures the average share price you obtained the stock/mutual fund for. It does not measure the effect of total wealth based on the return the investment offers you, which to you as an investor is what you really care about. Unfortunately, the net wealth obtained from this strategy is path dependent. That is, the net wealth depends upon the history of the return over the investing period of your investment horizon, 10 months in this example.
To prove this to myself I ran a half million Monte Carlo simulations for three distinct return strategies. One where the average return over the 12 months was zero, one where it was biased toward slightly negative returns and one where it was biased to slightly higher returns over the period of investing. A single simulation went like this. I generated random returns over 250 days where each day could have a random return selected between -5% and 5% and everywhere in between. For each 250 day period, I cost averaged 12 investments equally spaced of a single dollar. I measured the cumulative return of this strategy. I also invested $12 dollars all at once in the beginning of the 250 day period and measured its return. I then compared the difference between the two strategies. I did this for 500,000, 250 day periods.
Then I did the identical experiment where the returns were randomly selected between -5.5% and 5%, to get a slightly negative overall return bias then again for returns selected randomly between -5% and 5.5% to obtain the slightly positive return bias. I tabulated the returns and the time-series of returns and show the chart below documenting the results. The average returns were -0.25%, 0% and 0.25% across all half million returns, but the paths to obtain these average returns varied.
Now to help the reader understand these results, I draw your attention to the numbers highlighted in yellow in the chart below. This is the mean and median return difference between cost averaging (DCA) and lump sum investing for each of the three sets of simulations. Take the first experiment where we had a positive bias in the returns. In this scenario, the difference is negative meaning that if you have a positive return over the investing horizon, you’d obtain $24 out of your original $12 investment and the dollar cost averaging would have offered only $18 on your investment (on average) over the time period of the investment horizon. Hence, the difference is negative here and lump sum investing wins.The next experiment in the middle of the chart shows that you’d have obtained about the same returns for each strategy (within numerical error). Now look too the last chart where returns have a negative bias now. Here, the cost averaging method wins because you would suffer less losses over time, keeping some of your investment in cash while markets are going down. If you had invested the lump sum all at once in the beginning of the investment period here, you’d have more money subjected to negative returns and hence less wealth at the end of the investment horizon.
These numbers are unarguable about the path dependence of returns that determines whether cost averaging or lump sum investing is the better issue. Of course when saving for retirement, one has no choice but to cost average into your retirement investment. I haven’t met an employer yet who said on day one of employment, “here’s your 30 years salary in one lump sum payment”, so 401(k) is a savings plan everybody should avail oneself of regardless.
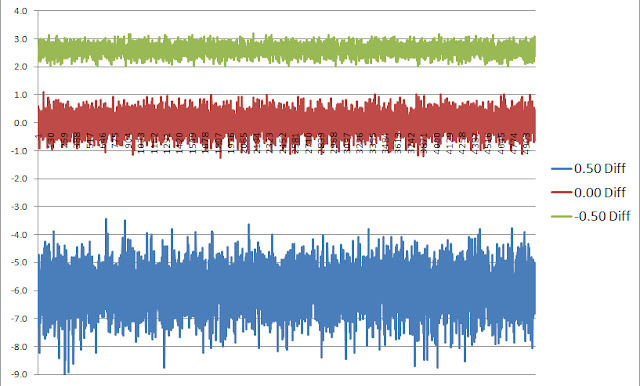
These numbers hide the time-series of returns of course over the 500,000 simulations because we only show average values and its enlightening to examine those returns due to the breadth or dispersion of values around the mean numbers. The chart below plots the 500,000 (truncated) individual simulation difference between 250 day, 12 investment cost averaging strategy versus lump sum investing, for the positive bias in blue, the negative bias in green and the zero return strategy in red.From this chart, one can see the much wider standard deviation of the positive bias (blue) outcomes than the negative bias (green) outcomes. This is very meaningful so let me explain. If the return over the investing horizon is positive, this example demonstrates that the possible return of lump sum investing over the cost averaging strategy could roughly be between 4% to 8%. While if the returns are negatively biased by the same amount the returns were positively biased, the spread between the cost averaging beating lump sum investing is only between 2% to 3%, a much lower dispersion. Due to the effect of compounding of returns, the path dependency impact of which one is the better strategy favors lump sum investing over cost averaging.
So in conclusion, this means the amount you’d better lump sum investing by when returns are negative by cost averaging, is much less than the amount you’d win by lump sum investing when returns are positive by the same amount. Since no one knows the future returns over the next investing horizon, it could be positive or negative, however the odds are in your favor to lump sum invest rather than cost average the lottery winnings simply because the gains you’d attain lump sum investing are much larger than the gain you’d attain cost averaging if returns are positive rather than negative.
No comments:
Post a Comment
Note: Only a member of this blog may post a comment.